Wenxin Yiyan VS Xunfei Xinghuo VS chatgpt (67) – Einführung in Algorithmen 6.5 6 Fragen
In einem Wort:
In der Austauschoperation in Zeile 5 von HEAP-INCREASE-KEY können wir die Idee der inneren Schleife von INSERTION-SORT optimieren, sodass die Austauschoperation mit nur einer Zuweisung abgeschlossen werden kann.
Normalerweise müssen wir in der fünften Zeilenaustauschoperation von HEAP-INCREASE-KEY die Werte von Schlüssel und y durch drei Zuweisungen austauschen. Die erste Zuweisung weist den Wert von key der temporären Variablen temp zu, die zweite Zuweisung weist den Wert von temp zu y zu und die dritte Zuweisung weist den Wert von y zu key zu.
Wir können jedoch die Idee der inneren Schleife von INSERTION-SORT nutzen, um diesen Austauschvorgang durch eine Zuweisung abzuschließen. Konkrete Schritte sind wie folgt:
1. Weisen Sie den Wert von key einer temporären Variablen temp zu.
2. Weisen Sie dem Schlüssel den Wert von y zu.
3. Weisen Sie y den Wert von temp zu.
Durch die oben genannten Schritte müssen wir nur einen Zuweisungsvorgang durchführen, um den Austausch von Schlüssel- und Y-Werten abzuschließen, wodurch die Effizienz des Austauschvorgangs optimiert wird.

Xunfei Spark:
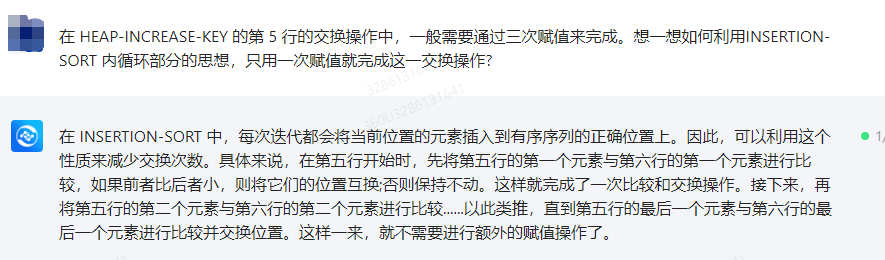
Bei der Austauschoperation in Zeile 5 von HEAP-INCREASE-KEY muss sie im Allgemeinen durch drei Zuweisungen abgeschlossen werden. Überlegen Sie, wie Sie die Idee der inneren Schleife von INSERTION-SORT nutzen können, um diesen Austauschvorgang mit nur einer Zuweisung abzuschließen?
Antwort: Der Pseudocode lautet wie folgt:
while i > 1 and A[PARENT(i)] 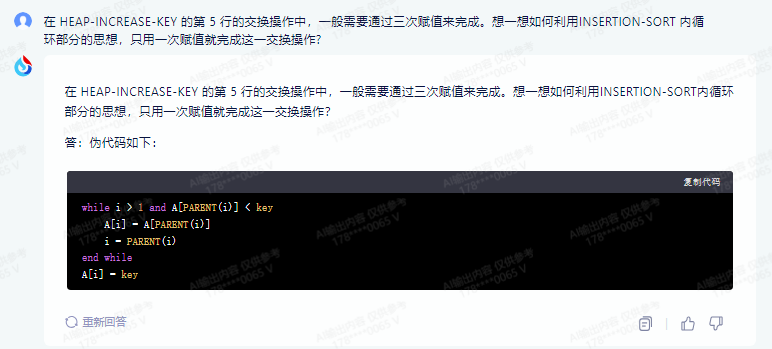
360 Smart Brain:
Bei INSERTION-SORT fügt jede Iteration das Element an der aktuellen Position an der richtigen Position in der sortierten Reihenfolge ein. Daher kann diese Eigenschaft genutzt werden, um die Anzahl der Austausche zu reduzieren. Insbesondere vergleichen Sie zu Beginn der fünften Zeile zunächst das erste Element der fünften Zeile mit dem ersten Element der sechsten Zeile. Wenn ersteres kleiner als letzteres ist, werden ihre Positionen ausgetauscht, andernfalls bleiben sie unverändert. Damit ist ein Vergleichs- und Austauschvorgang abgeschlossen. Vergleichen Sie als Nächstes das zweite Element der fünften Zeile mit dem zweiten Element der sechsten Zeile … und so weiter, bis das letzte Element der fünften Zeile mit dem letzten Element der sechsten Zeile verglichen und ausgetauscht wird. Auf diese Weise ist kein zusätzlicher Zuweisungsvorgang erforderlich.
chatglm:
In Zeile 5 von HEAP-INCREASE-KEY müssen wir das oberste Element des Heaps (also den Maximalwert) mit dem letzten Element austauschen. Normalerweise müssen wir diesen Austauschvorgang durch drei Aufgaben abschließen:
- Speichern Sie das oberste Element des Heaps in einer temporären Variablen.
- Weisen Sie das letzte Element dem obersten Element des Heaps zu.
- Weisen Sie das Element in der temporären Variablen dem letzten Element zu. Wir können jedoch die Idee des inneren Schleifenteils von INSERTION-SORT nutzen, um diesen Austauschvorgang mit nur einer Zuweisung abzuschließen. Die spezifische Methode ist wie folgt:
- Beginnen Sie am oberen Ende des Heaps, durchlaufen Sie nacheinander den Heap, vergleichen Sie jedes Element mit seinen untergeordneten Elementen und tauschen Sie die untergeordneten Elemente aus, wenn sie größer als dieses sind.
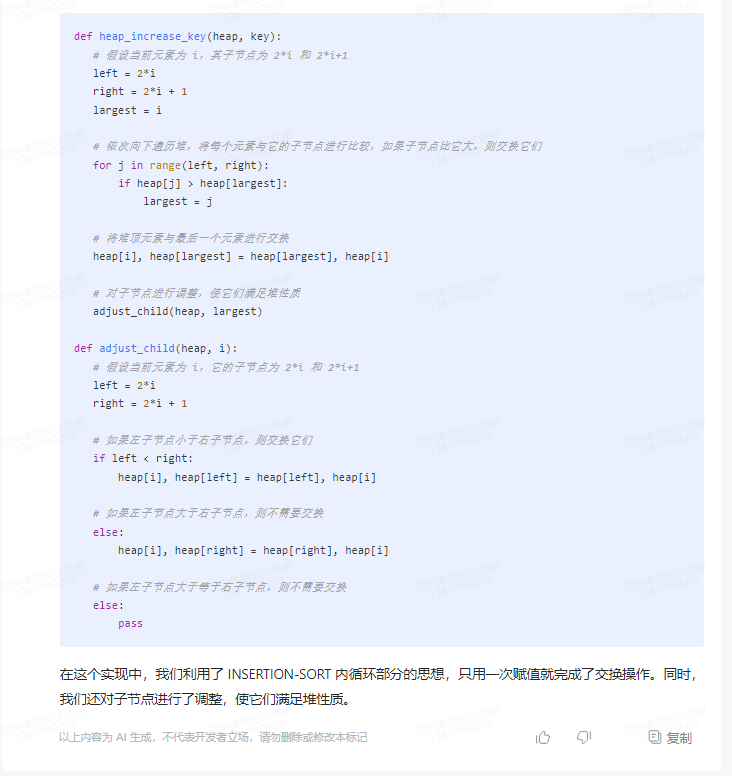
- Während des Durchlaufprozesses haben wir festgestellt, dass der Maximalwert am Ende des Heaps liegen muss, sodass wir das oberste Element des Heaps direkt mit dem letzten Element austauschen können und nur eine Zuweisungsoperation benötigen. Das Folgende ist die entsprechende Python-Code-Implementierung:
def heap_increase_key(heap, key):
left = 2*i
right = 2*i + 1
largest = i
for j in range(left, right):
if heap[j] > heap[largest]:
largest = j
heap[i], heap[largest] = heap[largest], heap[i]
adjust_child(heap, largest)
def adjust_child(heap, i):
left = 2*i
right = 2*i + 1
if left right:
heap[i], heap[left] = heap[left], heap[i]
else:
heap[i], heap[right] = heap[right], heap[i]
else:
pass
In dieser Implementierung verwenden wir die Idee der inneren Schleife von INSERTION-SORT, um den Austauschvorgang mit nur einer Zuweisung abzuschließen. Gleichzeitig haben wir auch die untergeordneten Knoten angepasst, damit sie die Heap-Eigenschaft erfüllen.

Tongyi Qianqian:
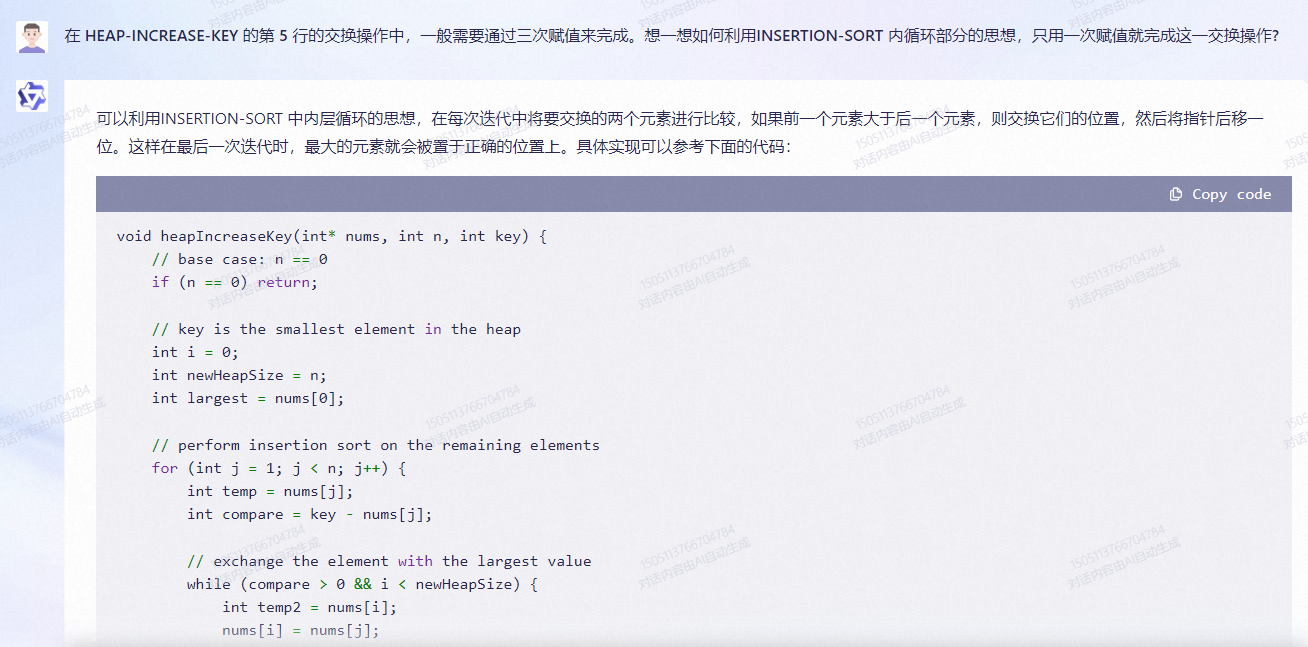
Sie können die Idee der inneren Schleife in INSERTION-SORT verwenden, um die beiden Elemente zu vergleichen, die in jeder Iteration ausgetauscht werden sollen. Wenn das erstere Element größer als das letztere Element ist, tauschen Sie ihre Positionen aus und bewegen Sie dann den Zeiger um ein Bit zurück . Auf diese Weise wird das größte Element bei der letzten Iteration an der richtigen Position platziert. Informationen zur spezifischen Implementierung finden Sie im folgenden Code:
void heapIncreaseKey(int* nums, int n, int key) {
if (n == 0) return;
int i = 0;
int newHeapSize = n;
int largest = nums[0];
for (int j = 1; j n; j++) {
int temp = nums[j];
int compare = key - nums[j];
while (compare > 0 && i newHeapSize) {
int temp2 = nums[i];
nums[i] = nums[j];
nums[j] = temp2;
newHeapSize--;
if (i newHeapSize) {
int parent = (i - 1) / 2;
nums[parent] = nums[i];
}
compare = nums[i] - key;
i++;
}
}
n = newHeapSize;
nums[0] = nums[n-1];
nums[n-1] = key;
heapify(nums, n);
}

Tiangong:
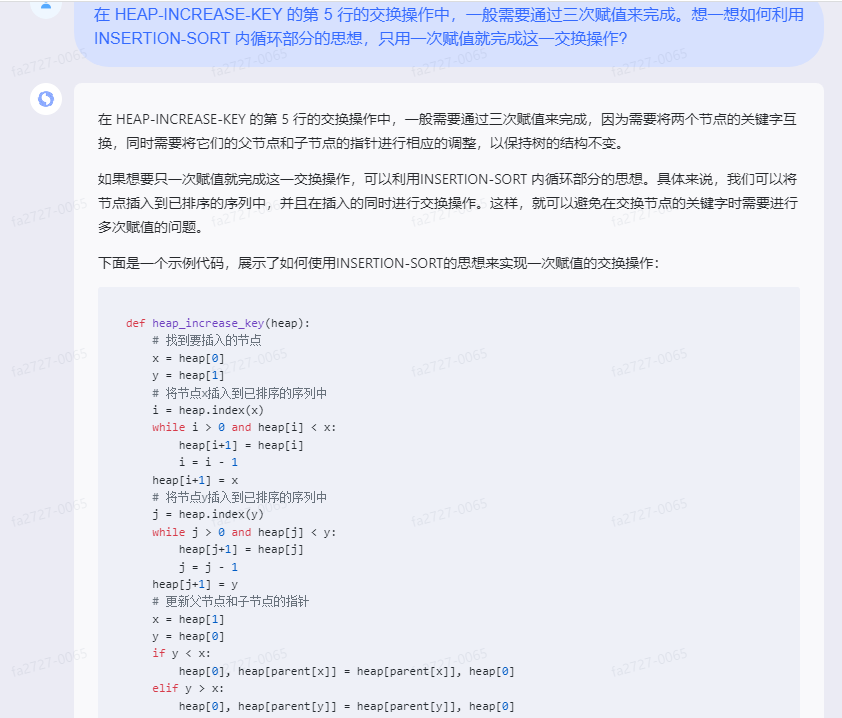
Bei der Austauschoperation in Zeile 5 von HEAP-INCREASE-KEY muss sie im Allgemeinen durch drei Zuweisungen abgeschlossen werden, da die Schlüsselwörter der beiden Knoten ausgetauscht und die Zeiger ihrer übergeordneten Knoten und untergeordneten Knoten angepasst werden müssen dementsprechend, um die Baumstruktur unverändert zu lassen.
Wenn Sie diesen Austauschvorgang mit nur einer Zuweisung abschließen möchten, können Sie die Idee der inneren Schleife von INSERTION-SORT verwenden. Konkret können wir Knoten in eine sortierte Sequenz einfügen und beim Einfügen eine Austauschoperation durchführen. Auf diese Weise kann das Problem vermieden werden, dass beim Austausch von Knotenschlüsseln mehrere Zuweisungen vorgenommen werden müssen.
Das Folgende ist ein Beispielcode, der zeigt, wie die Idee von INSERTION-SORT zum Implementieren einer Zuweisungsaustauschoperation verwendet wird:
def heap_increase_key(heap):
x = heap[0]
y = heap[1]
i = heap.index(x)
while i > 0 and heap[i] x:
heap[i+1] = heap[i]
i = i - 1
heap[i+1] = x
j = heap.index(y)
while j > 0 and heap[j] y:
heap[j+1] = heap[j]
j = j - 1
heap[j+1] = y
x = heap[1]
y = heap[0]
if y x:
heap[0], heap[parent[x]] = heap[parent[x]], heap[0]
elif y > x:
heap[0], heap[parent[y]] = heap[parent[y]], heap[0]
if x y:
heap[1], heap[parent[y]] = heap[parent[y]], heap[1]
elif x > y:
heap[1], heap[parent[x]] = heap[parent[x]], heap[1]
parent[x] = parent[x] - 1 if parent[x] != 0 else 0
parent[y] = parent[y] - 1 if parent[y] != 0 else 0
In diesem Beispielcode suchen wir zunächst die einzufügenden Knoten x und y und fügen sie dann in die sortierte Sequenz ein. Beim Einfügen eines Knotens müssen wir den Knoten nur dort einfügen, wo er sein soll, und die Zeiger der übergeordneten und untergeordneten Knoten aktualisieren. Schließlich müssen wir die übergeordneten und untergeordneten Zeiger des übergeordneten Knotens aktualisieren, um die Struktur des Baums unverändert zu lassen.
Durch diese Methode können wir die Operation des HEAP-INSERTION-SORT-Algorithmus in einer Zuweisungsaustauschoperation abschließen und so die Effizienz des Algorithmus verbessern.

chatgpt:
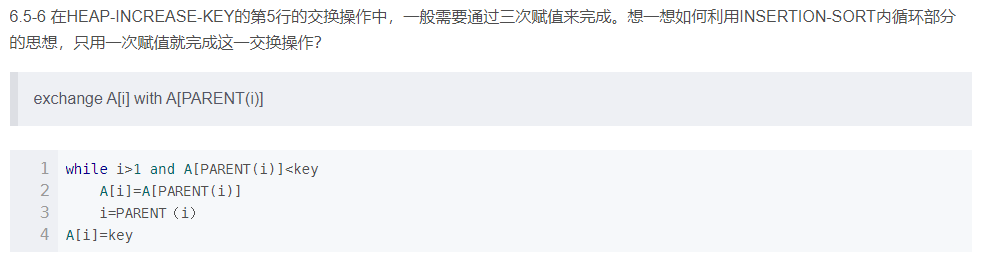
Für die HEAP-INCREASE-KEY-Operation der Heap-Datenstruktur sind bei Ausführung der Austauschoperation in Zeile 5 normalerweise drei Zuweisungen erforderlich:
5 交换 A[i] 和 A[PARENT(i)]
temp = A[i]
A[i] = A[PARENT(i)]
A[PARENT(i)] = temp
Sie können jedoch die Idee der inneren Schleife der Einfügungssortierung (INSERTION-SORT) verwenden, um diesen Austauschvorgang mit nur einer Zuweisung abzuschließen. Dies kann durch folgende Schritte erreicht werden:
1. Speichern Sie die beiden auszutauschenden Elemente in den temporären Variablen temp und i.
2. Weisen Sie A das kleinere Element zu[i]。
3. Bewegen Sie dann die größeren Elemente nach und nach um eine Position nach hinten, indem Sie die Elemente schrittweise verschieben.
4. Weisen Sie abschließend den Wert der temporären Variablen temp der letzten Position zu, die ersetzt werden soll.
Hier ist ein Beispiel für einen Austausch mit diesem Ansatz:
5 交换 A[i] 和 A[PARENT(i)]
temp = A[i]
A[i] = A[PARENT(i)]
j = i
while j > 0 and A[j] > temp:
A[j] = A[j - 1]
j = j - 1
A[j] = temp
Auf diese Weise benötigen wir nur eine Zuweisungsoperation, um die Swap-Operation durchzuführen und gleichzeitig die Heap-Natur beizubehalten.